Rädler Group
Soft Condensed Matter - Biological Physics - Nanoagents
Liedl Group
DNA Nanotechnology - Plasmonics
Nickel Group
Organic Electronics - X-ray Diffraction
Serwane Group
Mechanobiology - Neuronal networks
-
 Snowy Greetings from Antholz (IT)
Snowy Greetings from Antholz (IT)Our annual Winter School in Antholz is right now happening. Every Member of the chair is giving a presentation in the heart of South Tyrol. Not only is there a scientific competition, but everyone will face each other in the traditional biathlon.
-
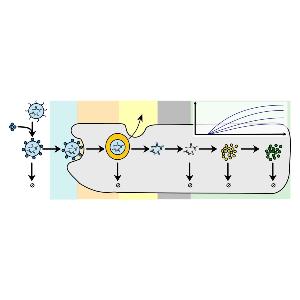 Rädler Group: new review on LNPs and protein expression
Rädler Group: new review on LNPs and protein expressionCheck it out in the European Journal of Pharmaceutics and Biopharmaceutics
-
New publication in the Rädler Group
pH-dependent structural transitions in cationic ionizable lipid mesophases are critical for lipid nanoparticle function